Kontent qismiga oʻtish

Kartogramma

Vikipediya, ochiq ensiklopediya
Dunyo aholisining kartogrammasi

Kartogramma (shuningdek, nemis tilida soʻzlashuvchilar orasida keng tarqalgan, qiymatli hudud xaritasi yoki anamorfik xarita deb ham ataladi) — geografik oʻlchami oʻzgartirilgan obyektlar (mamlakatlar, viloyatlar va boshqalar) toʻplamining tematik xaritasi boʻlib, sayohat vaqti, aholi yoki YaIM kabi tanlangan nisbat darajasidagi oʻzgaruvchiga toʻgʻridan-toʻgʻri proportsionaldir. Geografik makonning oʻzi shunday qilib, oʻzgaruvchining taqsimlanishini tasavvur qilish uchun baʼzan haddan tashqari buziladi. Bu xaritaning eng mavhum turlaridan biri; Aslida, baʼzi shakllarni diagrammalar deb atash mumkin. Ular, birinchi navbatda, diqqatni tortish va nomograflar sifatida tahlil qilish uchun ishlatiladi.[1]

Kartogrammalar o'lcham umumiy miqdorni ifodalash uchun eng intuitiv vizual o'zgaruvchidir.[2] Bunda u nuqta xususiyatlarini masshtablashtirgan proportsional belgilar xaritalariga va chiziqli xususiyatlarning og'irligini o'lchaydigan ko'plab oqim xaritalariga o'xshash strategiyadir. Biroq, bu ikki usul faqat xarita belgisini masshtablaydi, fazoning o'zini emas; chiziqli obyektlar uzunligini uzaytiruvchi xarita chiziqli kartogramma hisoblanadi (garchi qo'shimcha oqim xaritasi texnikasi qo'shilishi mumkin). Tuzilgandan so'ng, kartogrammalar ko'pincha xoroplet xaritasi kabi qo'shimcha o'zgaruvchilarni vizualizatsiya qilish uchun boshqa tematik xaritalash usullari uchun asos sifatida ishlatiladi.

Tarixi

[tahrir | manbasini tahrirlash]
Levasseurning Yevropa kartogrammasi

Kartogramma tematik xaritalarning boshqa turlariga qaraganda kechroq ishlab chiqilgan, lekin Fransiyada bir xil innovatsiya anʼanalariga amal qilgan.[3] Maʼlum boʻlgan eng qadimgi kartogramma 1876-yilda fransuz statistik va geograf Pierre Émile Levasseur tomonidan nashr etilgan boʻlib, u Yevropa mamlakatlarini kvadrat shaklida aks ettiruvchi, oʻzgaruvchiga koʻra oʻlchamdagi va umumiy geografik joylashuvi boʻyicha joylashtirilgan (alohida xaritalar bilan masshtablangan) bir qator xaritalarni yaratgan.[4] Keyinchalik sharhlovchilar uning raqamlarini xarita emas, balki statistik diagramma deb atashdi, lekin Levasseur uni karta majoziy deb atagan, oʻsha paytda har qanday tematik xarita uchun ishlatiladigan umumiy atama. U ularni oʻquv qoʻllanmasi sifatida ishlab chiqardi va oʻlchamning intuitiv kuchini vizual oʻzgaruvchanlik sifatida darhol tan oldi: "Bolani Gʻarbiy Yevropa savdosining Sharqiy Yevropaga nisbatan ahamiyati hayratda qoldirmasligi mumkin emas. Eʼtibor bering, kichik hududga ega, lekin boyligi va ayniqsa, dengiz floti boʻyicha boshqa xalqlardan qanchalar ustun turadi, aksincha, oʻz maydoni va aholisi boʻyicha birinchi oʻrinni egallagan Rossiya haligacha savdo va navigatsiya boʻyicha boshqa davlatlardan qanchalik ortda qolmoqda."

Levasseurning texnikasi boshqalar tomonidan qabul qilinmagan koʻrinadi va koʻp yillar davomida nisbatan kamroq shunga oʻxshash xaritalar paydo boʻladi. Keyingi eʼtiborga molik ishlanma 1903-yilgi saylovga tayyorgarlik koʻrish uchun Germaniya Reyxstagi uchun 1898-yilgi saylov natijalarining Hermann Haack va Hugo Weichel tomonidan yaratilgan bir juft xarita edi, bu eng qadimgi maʼlum boʻlgan qoʻshni kartogramma hisoblanadi.[5] Ikkala xaritada ham Germaniya imperiyasining oʻxshash konturi koʻrsatilgan boʻlib, ulardan biri masshtabga qarab okruglarga boʻlingan, ikkinchisi esa hudud boʻyicha saylov okruglarini tuzib koʻrsatgan. Keyinchalik Berlin, Gamburg va Saksoniya atrofidagi aholi zich joylashgan hududlarning kengayishi asosan shaharlik sotsial-demokratlarning xalq ovozida gʻalaba qozonish uchun munozarali tendensiyasini tasavvur qilish uchun moʻljallangan edi, ayni paytda asosan qishloqda joylashgan Zentrum koʻproq oʻrinlarni qoʻlga kiritdi (shunday qilib, kartogrammalarning zamonaviy mashhurligini oldindan aytib berdi). Amerika Qoʻshma Shtatlaridagi soʻnggi saylovlarda ham xuddi shunday tendensiyalarni koʻrsatilmoqda.[6]

Uzluksiz kartogramma koʻp oʻtmay Qoʻshma Shtatlarda paydo boʻldi, u yerda 1911-yildan keyin mashhur ommaviy axborot vositalarida paydo boʻldi.[7] Koʻpchilik xaritalar Haack va Weichel kartogrammalari bilan solishtirganda juda qoʻpol chizilgan edi, texnikani ixtiro qilganini daʼvo qilgan amerikalik usta kartograf Erwin Raiszning „toʻrtburchaklar statistik kartogrammalari“ bundan mustasno.[8] Haack va Weichel oʻz xaritalarini kartogramma deb atashganida, bu atama odatda barcha tematik xaritalarga, ayniqsa Yevropada ishlatilganlarga nisbatan qoʻllangan.[9] Raisz va boshqa akademik kartograflar oʻzlarining darsliklarida ushbu atamaning cheklangan foydalanishni afzal koʻrishlarini bildirganlaridan keyingina (Raisz dastlab qiymat maydoni kartogrammasini qoʻllab-quvvatlagan) hozirgi maʼno asta-sekin qabul qilingan.[10]

Kartogrammalarning asosiy vazifasi har doim buzilgan shakllarni yaratish boʻlib, ularni kompyuterni avtomatlashtirishning asosiy maqsadiga aylantirgan. Waldo R. Tobler 1963-yilda birinchi algoritmlardan birini ishlab chiqdi, u alohida tumanlardan koʻra fazoning oʻzini burish strategiyasiga asoslandi.[11] Oʻshandan beri turli xil algoritmlar ishlab chiqildi (pastga qarang), garchi hali ham kartogrammalarni qoʻlda yaratish odatiy holdir.

Hudud kartogrammalari

[tahrir | manbasini tahrirlash]
Germany kartogrammasi

Hudud kartogrammasi eng keng tarqalgan shakldir; u mintaqaviy xususiyatlar toʻplamini, odatda okruglar yoki mamlakatlar kabi maʼmuriy tumanlarni oʻlchaydi, shuning uchun har bir tumanning maydoni berilgan oʻzgaruvchiga toʻgʻridan-toʻgʻri proportsionaldir. Odatda bu oʻzgaruvchi umumiy aholi soni, yalpi ichki mahsulot yoki maʼlum bir tovar yoki turdagi chakana savdo doʻkonlari soni kabi biror narsaning umumiy sonini yoki miqdorini ifodalaydi. Aholi jon boshiga toʻgʻri keladigan YaIM yoki tugʻilish darajasi kabi boshqa qatʼiy ijobiy nisbat oʻzgaruvchilari ham ishlatilishi mumkin, ammo ular baʼzan oʻlchamni umumiy miqdor sifatida talqin qilishning tabiiy tendentsiyasi tufayli notoʻgʻri natijalar berishi mumkin. Ulardan umumiy aholi soni, ehtimol, eng keng tarqalgan oʻzgaruvchi boʻlib, baʼzan izodemografik xarita deb ataladi.

Turli strategiyalar va algoritmlar, odatda, shakl va topologiyani saqlash boʻyicha strategiyalariga koʻra, bir necha usullar bilan tasniflangan. Shaklni saqlaydiganlar baʼzan ekviform deb ataladi, ammo izomorf (bir xil shaklli) yoki gomomorfik (oʻxshash shakl) yaxshiroq atamalar boʻlishi mumkin. Uchta keng toifa keng tarqalgan: qoʻshni (topologiyani saqlash, shaklni buzish), qoʻshni boʻlmagan (shaklni saqlash, topologiyani buzish) va diagrammatik (ikkalini ham buzish). Soʻnggi paytlarda Nusrat va Koburov, Markovska va boshqalar tomonidan taklif qilingan yondashuvlar va natijalarning koʻrinishidagi xilma-xillikni qoʻlga kiritish uchun ushbu asosiy asosga asoslanib, yanada chuqurroq taksonomiyalar yaratildi.[12] Turli taksonomiyalar hududiy kartogrammalarning quyidagi umumiy turlari boʻyicha kelishib olishga moyildirlar.

Anamorfik proyeksiya

[tahrir | manbasini tahrirlash]

Bu alohida xususiyatlarni buzishdan koʻra, tanlangan oʻzgaruvchining fazoviy taqsimotini tenglashtirish uchun fazoning oʻzini buzish uchun yagona parametrik matematik formuladan (masalan, polinom egri sirt) foydalanadigan qoʻshni kartogrammaning bir turi. Bu farq tufayli baʼzilar natijani psevdokartogramma deb atashni afzal koʻrishgan.[13] Toblerning birinchi kompyuter kartogrammasi algoritmi shu strategiyaga asoslangan edi,[14] buning uchun u oʻzining va keyingi algoritmlari asoslangan umumiy matematik konstruksiyani ishlab chiqdi. Ushbu yondashuv birinchi navbatda tanlangan oʻzgaruvchining uzluksiz zichlik funktsiyasi sifatida taqsimlanishini modellashtiradi (odatda eng kichik kvadratlar moslamasi yordamida), soʻngra zichlik tenglashtirilgan boʻlishi uchun boʻshliqni sozlash uchun ushbu funktsiyaning teskarisidan foydalanadi. Gastner-Nyuman algoritmi, bugungi kunda eng mashhur vositalardan biri, bu yondashuvning yanada rivojlangan versiyasidir. Ular tumanlarni toʻgʻridan-toʻgʻri masshtablashtirmagani uchun har bir tumanning maydoni uning qiymatiga toʻliq teng ekanligiga kafolat yoʻq.[15]

Shaklni oʻzgartiruvchi qoʻshni kartogrammalar

[tahrir | manbasini tahrirlash]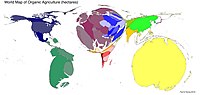
Qoʻshni kartogramma

Noqonuniy kartogrammalar yoki deformatsiya kartogrammalari deb ham ataladi.[16] Bu juda turli xil algoritmlar oilasi boʻlib, u qoʻshni qirralarni saqlab, har bir tumanning shaklini oʻlchaydi va deformatsiya qiladi. Bu yondashuv XX asr boshlarida Haack hamda Weichel va boshqalarning kartogrammalaridan kelib chiqqan, garchi ular hozirgi kompyuterlashtirilgan versiyalar kabi matematik jihatdan aniq boʻlsa ham. Taklif etilgan yondashuvlarning xilma-xilligiga uyali avtomatlar, toʻrtburchaklar boʻlinishlari, kartografik umumlashtirish, medial oʻqlar, bahorga oʻxshash kuchlar va inflyatsiya va deflyatsiya simulyatsiyasi kiradi. Baʼzilar asl shaklning qandaydir oʻxshashligini saqlab qolishga harakat qilishadi (va shuning uchun uni gomomorf deb atash mumkin),[17] lekin bu koʻpincha shaklni jiddiy buzadiganlarga qaraganda ancha murakkab va sekinroq algoritmlardir.

Qoʻshni boʻlmagan izomorf kartogrammalar

[tahrir | manbasini tahrirlash]

Bu, ehtimol, kartogramma tuzishning eng oddiy usuli boʻlib, unda har bir tuman shaklini umuman oʻzgartirmasdan, oʻzgaruvchiga koʻra oddiygina kichraytiriladi yoki kattalashtiriladi. Koʻpgina hollarda, ikkinchi qadam shakllar orasidagi boʻshliqlar va bir-birining ustiga chiqishini kamaytirish uchun har bir shaklning joylashishini moslashtiradi, lekin ularning chegaralari aslida qoʻshni emas. Shaklni saqlash ushbu yondashuvning asosiy afzalligi boʻlsa-da, natijalar koʻpincha tasodifiy koʻrinishga ega boʻladi, chunki alohida tumanlar bir-biriga yaxshi mos kelmaydi.

Diagrammatik (Dorling) kartogrammalar

[tahrir | manbasini tahrirlash]
Diagrammatik (Dorling) kartogramma

Ushbu yondashuvda har bir tuman proportsional oʻlchamdagi oddiy geometrik shakl bilan almashtiriladi. Shunday qilib, asl shakl butunlay yoʻq qilinadi va qoʻshnilik cheklangan shaklda saqlanishi yoki umuman boʻlmasligi mumkin. Garchi Daniel Dorlingning 1996-yildagi algoritmi birinchi marta qurilishini osonlashtirganidan keyin ular odatda Dorling kartogrammalari deb atalsa-da,[18] bu aslida Levasseur (1876) va Raisz (1934) davridagi kartogrammaning asl shaklidir.[19] Geometrik shakllar uchun bir nechta variant mavjud:

  • Doirali (Dorling), odatda teginish uchun birlashtiriladi va asl makonning umumiy shakliga oʻxshashlikni saqlab qolish uchun tartibga solinadi. Ular koʻpincha proportsional belgili xaritalarga oʻxshaydi va baʼzilar ularni tematik xaritaning ikki turi oʻrtasidagi gibrid deb hisoblashadi.
  • Kvadratchali (Levasseur/Demers), aylanalar bilan bir xil tarzda muomala qilinadi, garchi ular odatda oddiy tarzda bir-biriga mos kelmasa ham.
  • Toʻrtburchakli (Raisz), unda har bir toʻrtburchaklar tumanning balandligi va kengligi umumiy shaklga mos keladigan tarzda sozlanadi. Natija daraxt xaritasi diagrammasiga oʻxshaydi, garchi ikkinchisi odatda geografiya emas, balki hajmi boʻyicha tartiblangan. Ular koʻpincha qoʻshni boʻladi, garchi qoʻshnilik xayoliy boʻlishi mumkin, chunki xaritada qoʻshni boʻlgan koʻplab tumanlar haqiqatda qoʻshni boʻlgan tumanlar bilan bir xil boʻlmasligi mumkin.

Tumanlar umuman tanib boʻlmaydiganligi sababli, bu yondashuv xarita oʻquvchilariga har qanday shakllar tanish boʻlmagan vaziyatlarda (masalan, Buyuk Britaniya parlament saylov okruglari) yoki tumanlar xaritani oʻqiydiganlarga shunchalik tanish boʻlgan holatlarda eng foydali va mashhurdir. Odatda, bu usul oʻquvchilar uchun alohida tumanlarni aniqlashdan koʻra umumiy geografik naqshni aniqlash muhimroq boʻlganda qoʻllanadi; agar identifikatsiya zarur boʻlsa, individual geometrik shakllar koʻpincha etiketlanadi.

Mahsulotlar

[tahrir | manbasini tahrirlash]

Kompyuter vizualizatsiyasi yordamida kartogrammalarni yaratgan birinchi kartograflardan biri 1960-yillarda Santa Barbara universitetidan Waldo Tobler edi. Tobler ishidan oldin, kartogrammalar qoʻlda yaratilgan (baʼzilari hali ham mavjud). UCSB kampusida joylashgan Milliy geografik maʼlumot va tahlil markazida kartogrammalarga oid resurslarga ega onlayn Cartogram Central mavjud.

Bir qator dasturiy paketlar kartogrammalarni yaratadi. Mavjud kartogramma yaratish vositalarining koʻpchiligi boshqa GIS dasturiy vositalari bilan birgalikda qoʻshimchalar sifatida ishlaydi yoki keng tarqalgan GIS mahsulotlari bilan ishlash uchun formatlangan GIS maʼlumotlaridan mustaqil ravishda kartografik natijalarni ishlab chiqaradi. Kartogramma dasturlariga misollar ScapeToad,Cart va Cartogram Processing Tool (ESRI’s ArcGIS uchun ArcScript), ularning barchasi Gastner-Newman algoritmidan foydalanadi.[20] Muqobil algoritm Carto3F ham Windows platformalarida notijorat maqsadlarda foydalanish uchun mustaqil dastur sifatida amalga oshiriladi.[21] Bu dastur, shuningdek, original Dougenik kauchuk varaq algoritmini optimallashtirishni ham taʼminlaydi.[22] CRAN toʻplamining Rec-Mapi to'rtburchaklar kartogramma algoritmini amalga oshirishni taʼminlaydi.[23]

Algoritmlar

[tahrir | manbasini tahrirlash]
Yil Muallif Algoritm Turi Shakli Topologiyasi
1973 Waldo R. Tobler Rubber xarita usuli hudud qoʻshni boʻlmagan Bor, lekin kafolatlanmagan
1976 Olson Proyektor usuli hudud shaklli Yoʻq
1978 Kadmon, Shlomi Polifokal proyeksiya radial masofa maʼlum boʻlmagan maʼlum boʻlmagan
1984 Selvin et al. DEMP (radial kengayish) usuli hudud qoʻshni boʻlmagan maʼlum boʻlmagan
1985 Dougenik et al. Kauchuk varaqni buzish usuli hudud qoʻshni boʻlmagan Bor, lekin kafolatlanmagan
1986 Waldo R. Tobler Psevdokartogramma usuli hudud qoʻshni boʻlmagan Bor
1987 Snyder Kattalashtiruvchi shisha azimutal xarita proyeksiyalari radial masofa maʼlum boʻlmagan maʼlum boʻlmagan
1989 Cauvin et al. Piezoplet xaritalar hudud qoʻshni boʻlmagan maʼlum boʻlmagan
1990 Torguson Interaktiv koʻpburchak ziplash usuli hudud qoʻshni boʻlmagan maʼlum boʻlmagan
1990 Danny Dorling Uyali avtomatlashtirish mashinasi usuli hudud qoʻshni boʻlmagan Bor
1993 Gusein-Zade, Tikunov Chiziqli integral usuli hudud qoʻshni boʻlmagan Bor
1996 Danny Dorling Doiraviy kartogramma hudud doirali Yoʻq
1997 Sarkar, Brown Baliq koʻzining grafik koʻrinishlari radial masofa maʼlum boʻlmagan maʼlum boʻlmagan
1997 Herbert Edelsbrunner, Waupotitsch Kombinatorga asoslangan yondashuv usuli hudud qoʻshni boʻlmagan maʼlum boʻlmagan
1998 Kocmoud, House Cheklovga asoslangan yondashuv usuli hudud qoʻshni boʻlmagan Bor
2001 Daniel A. Keim, North, Panse KartoDraw usuli hudud qoʻshni boʻlmagan Bor, algoritmik kafolatlangan
2004 Gastner, Newman Diffuziyaga asoslangan usul hudud qoʻshni boʻlmagan Bor, algoritmik kafolatlangan
2004 Sluga Cheklovga asoslangan yondashuv usuli hudud qoʻshni boʻlmagan maʼlum boʻlmagan
2004 van Kreveld, Speckmann Toʻrtburchakli kartogramma usuli hudud toʻrtburchakli Yoʻq
2004 Heilmann, Daniel A. Keim RecMap usuli hudud toʻrtburchakli Yoʻq
2005 Daniel A. Keim, North, Panse Medial oʻqga asoslangan kartogrammalar hudud qoʻshni boʻlmagan Bor, algoritmik kafolatlangan
2009 Heriques, Bação, Lobo Karto-SOM usuli hudud qoʻshni boʻlmagan Bor
2013 Shipeng Sun Opti-DCN usuli hudud qoʻshni boʻlmagan Bor, algoritmik kafolatlangan
2014 B. S. Daya Sagar Matematik morfologiyaga asoslangan kartogrammalar hudud qoʻshni boʻlmagan Yoʻq
2018 Gastner, Seguy, More Tez oqimga asoslangan usul hudud qoʻshni boʻlmagan Bor, algoritmik kafolatlangan

Manbalar

[tahrir | manbasini tahrirlash]
  1. ↑ https://www.tandfonline.com/doi/abs/10.1111/j.1467-8306.2004.09401004.x
  2. ↑ Jacque Bertin, Sémiologie Graphique. Les diagrammes, les réseaux, les cartes. With Marc Barbut [et al.]. Paris : Gauthier-Villars. Semiology of Graphics, English Edition, Translation by William J. Berg, University of Wisconsin Press, 1983.)
  3. ↑ https://indiemaps.com/blog/2008/12/early-cartograms/
  4. ↑ https://babel.hathitrust.org/cgi/pt?id=uc1.c2558275
  5. ↑ Haack, Hermann; Weichel, Hugo (1903). Kartogramm zur Reichstagswahl. Zwei Wahlkarten des Deutschen Reiches. Justus Perthes Gotha.
  6. ↑ https://www.researchgate.net/publication/329880252_Kartogramm_zur_Reichstagswahl_An_early_electoral_cartogram_of_Germany
  7. ↑ https://archive.org/details/independent70newy/page/722/mode/2up
  8. ↑ https://www.tandfonline.com/doi/abs/10.1080/00221343608987880
  9. ↑ https://www.jstor.org/stable/301591
  10. ↑ https://makingmaps.net/2010/11/30/more-old-school-cartograms-1921-1938/
  11. ↑ https://www.jstor.org/stable/212809?origin=crossref
  12. ↑ https://www.sciendo.com/article/10.2478/pcr-2019-0005
  13. ↑ „arxiv nusxasi“. 2021-yil 29-yanvarda asl nusxadan arxivlangan. Qaraldi: 2022-yil 5-iyun.
  14. ↑ Tobler, Waldo R. (Jan 1963). „Geographic Area and Map Projections“. Geographical Review. 53 (1): 59-79
  15. ↑ https://www.ncbi.nlm.nih.gov/pmc/articles/PMC419634/
  16. ↑ https://www.sciendo.com/article/10.2478/pcr-2019-0005
  17. ↑ https://www.researchgate.net/publication/3788051_Continuous_cartogram_construction
  18. ↑ Dorling, Daniel (1996). Area Cartograms: Their Use and Creation. Concepts and Techniques in Modern Geography (CATMOG). Vol. 59. University of East Anglia.
  19. ↑ https://www.jstor.org/stable/208794?origin=crossref
  20. ↑ https://www.esri.com/news/arcuser/0110/cartograms.html
  21. ↑ http://sunsp.net/portfolio.html
  22. ↑ http://www-personal.umich.edu/~mejn/cart/
  23. ↑ https://web.archive.org/web/20130628092855/http://artofsoftware.org/2012/02/08/cartogram-crash-course/

Havolalar

[tahrir | manbasini tahrirlash]
"https://uz.wikipedia.org/w/index.php?title=Kartogramma&oldid=5188445" dan olindi