Binar daraxti

Binar daraxti ikkilik ifodalarni ifodalash uchun ishlatiladigan dastur tili hisoblanadi. Binar daraxti ifodalashi mumkin boʻlgan ikkita keng tarqalgan ikkilik ifoda turi algebraik va mantiqiy ifoda turlari hisoblanadi. Binar daraxti birlik va ikkilik operatorlarni oʻz ichiga olgan ifodalarni ifodalashi mumkin.

Binar ifoda daraxtining har bir tugunida nol, bitta yoki ikkita son mavjud. Ushbu cheklangan struktura ifoda daraxtlarini qayta ishlashni soddalashtiradi.

(a+b)*c+7 ifodaning ifodalar daraxti

Umumiy koʻrinishi

Ikkilik ifoda daraxtining barglari operandlar, masalan, doimiylar yoki oʻzgaruvchilar nomlari va boshqa tugunlarda operatorlar mavjud. Bu alohida daraxtlar ikkilik boʻladi, chunki barcha operatsiyalar ikkilikdir va bu eng oddiy holat boʻlsa-da, tugunlarda ikkitadan ortiq son boʻlishi mumkin. Bundan tashqari, birlik minus operatorida boʻlgani kabi, tugunning har biri faqat bitta songa ega boʻlishi mumkin. Ifodalar daraxti T ni chap va oʻng pastki daraxtlarni rekursiv baholash natijasida olingan qiymatlarga ildizdagi operatorni qoʻllash orqali baholash mumkin.

Oʻtish

Algebraik ifoda ikkilik ifoda daraxtidan qavs ichiga olingan chap ifodani rekursiv ishlab chiqarish, soʻngra operatorni ildizga chiqarish va nihoyat, qavs ichiga olingan oʻng ifodani rekursiv ishlab chiqarish orqali ishlab chiqarilishi mumkin. Ushbu umumiy strategiya (chap, tugun, oʻng) <b>tartibli o'tish</b> sifatida tanilgan. Muqobil oʻtish strategiyasi chap pastki daraxtni, oʻng pastki daraxtni va keyin operatorni rekursiv ravishda chop etishdir. Ushbu oʻtish strategiyasi odatda <b>buyruqdan keyingi o'tish</b> sifatida tanilgan. Uchinchi strategiya — avval operatorni chop etish, soʻngra oldindan tartibli oʻtkazish deb nomlanuvchi chap va oʻng pastki daraxtni rekursiv ravishda chop etish.

Ushbu uchta standartdan birinchi oʻtish uch xil ifoda formatlarining ifodasidir: infiks, postfiks va prefiks. Infiks ifodasi tartibni kesib oʻtish orqali, postfiks ifodasi buyruqdan keyingi oʻtish orqali va prefiks ifodasi oldindan tartibli oʻtish orqali hosil boʻladi.

Infiks oʻtish

Infiks ifodasi chop etilganda, har bir ifodaning boshiga va oxiriga ochilish va yopish qavslari qoʻshilishi kerak. Har bir pastki daraxt pastki ifodani ifodalaganligi sababli, uning boshida ochilish qavslari va barcha sonlarni qayta ishlagandan soʻng, yopish qavslari chop etiladi.

Psevdokod:

Algoritm infix ( daraxt )

Algorithm infix (tree)
/*Print the infix expression for an expression tree.
 Pre : tree is a pointer to an expression tree
 Post: the infix expression has been printed*/
 if (tree not empty)
  if (tree token is operator)
    print (open parenthesis)
  end if
  infix (tree left subtree)
  print (tree token)
  infix (tree right subtree)
  if (tree token is operator)
    print (close parenthesis)
  end if
 end if
end infix

Postfiksdan oʻtish

):):):):):):):):)::):):):):):):):):):):)::):):):):)

Algoritm postfiks ( daraxt )

Algorithm postfix (tree)
/*Print the postfix expression for an expression tree.
 Pre : tree is a pointer to an expression tree
 Post: the postfix expression has been printed*/
 if (tree not empty)
  postfix (tree left subtree)
  postfix (tree right subtree)
  print (tree token)
 end if
end postfix

Prefiks oʻtish

Psevdokod:

Algoritm prefiks ( daraxt )

Algorithm prefix (tree)
/*Print the prefix expression for an expression tree.
 Pre : tree is a pointer to an expression tree
 Post: the prefix expression has been printed*/
 if (tree not empty)
  print (tree token)
  prefix (tree left subtree)
  prefix (tree right subtree)
 end if
end prefix

Ifodalar daraxtini qurish

Daraxtning qurilishi postfiks ifodasini bir vaqtning oʻzida bitta belgini oʻqish orqali amalga oshiriladi. Agar belgi operand boʻlsa, bitta tugunli daraxt yaratiladi va uning koʻrsatkichi stekga suriladi. Agar belgi operator boʻlsa, ikkita T1 va T2 daraxtiga koʻrsatgichlar stekdan chiqariladi va ildizi operator boʻlgan va chap va oʻng sonlari mos ravishda T2 va T1 ni koʻrsatadigan yangi daraxt hosil boʻladi. Keyin ushbu yangi daraxtga koʻrsatgich stekka suriladi.

Misol

Postfiks yozuvidagi kirish: ab + cde + * * Birinchi ikkita belgi operandlar boʻlgani sababli, bitta tugunli daraxtlar yaratiladi va ularga koʻrsatgichlar stekga suriladi. Qulaylik uchun stek chapdan oʻngga oʻsadi.

Stek chapdan oʻngga oʻsadi

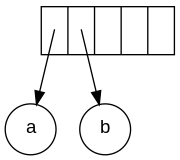
Keyingi belgi „+“ belgisidir. U ikkita koʻrsatgichni daraxtlarga koʻchiradi, yangi daraxt hosil boʻladi va unga koʻrsatgich stekga suriladi.

Yangi daraxtning shakllanishi

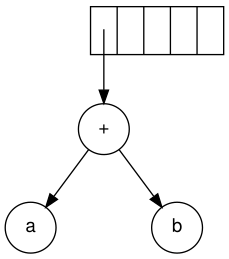
Keyin c, d va e oʻqiladi. Har biri uchun bitta tugunli daraxt yaratiladi va mos keladigan daraxtga koʻrsatgich stekga suriladi.

Bir tugunli daraxt yaratish

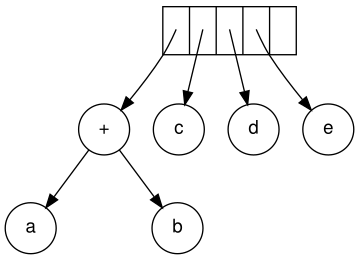
Davom etishda „+“ belgisi oʻqiladi va u oxirgi ikkita daraxtni birlashtiradi.

Ikki daraxtni birlashtirish

Endi „*“ oʻqiladi. Oxirgi ikkita daraxt koʻrsatkichi ochiladi va ildiz sifatida „*“ belgisi bilan yangi daraxt hosil boʻladi.

Ildiz bilan yangi daraxtni shakllantirish

Nihoyat, oxirgi belgi oʻqiladi. Ikki daraxt birlashtiriladi va oxirgi daraxtda koʻrsatgich stekda qoladi.

Ab + cde + * * ifoda daraxtini yaratish bosqichlari

((5 + z) / −8) * (4 ^ 2) ga ekvivalent ikkilik algebraik ifoda daraxti

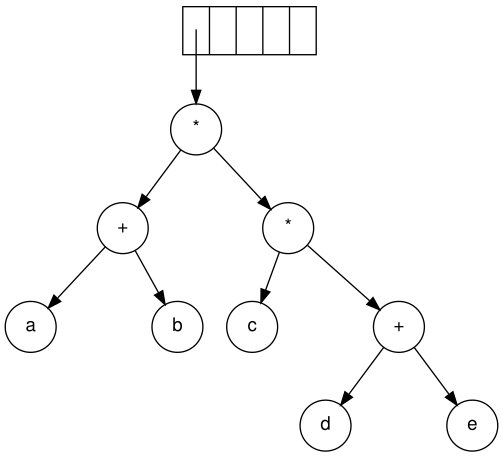
Algebraik ifodalar

Algebraik ifoda daraxtlari raqamlar, oʻzgaruvchilar va birlik va ikkilik operatorlarni oʻz ichiga olgan ifodalarni ifodalaydi. Baʼzi umumiy operatorlar × (koʻpaytirish), ÷ (boʻlish), + (qoʻshish), — (ayirish), ^ (koʻrsatkich) va — (inkor). Operatorlar daraxtning ichki tugunlarida, raqamlar va oʻzgaruvchilar barg tugunlarida joylashgan boʻladi. Ikkilik operatorlar tugunlarida ikkita tugun, birlik operatorlarda esa bitta tugun mavjud.

Ikkilik mantiqiy ifoda daraxtiga ekvivalent ((rost $\lor$ yolgʻon) $\land$$\neg$ yolgʻon) $\lor$ (rost $\lor$ yolgʻon))

Mantiqiy ifodalar

Mantiqiy ifodalar algebraik ifodalarga juda oʻxshash tarzda ifodalanadi, yagona farq maxsus qiymatlar va ishlatiladigan operatorlardir. Mantiqiy ifodalar oʻzgarmas qiymatlar sifatida true(rost) va false(yolgʻon) dan foydalanadi va quyidagi operatorlarni oʻz ichiga oladi: $\land$ (AND), $\lor$ (OR), $\neg$ (NOT).