Chelak argumenti
Isaak Nyutonning aylanuvchi chelak argumenti (shuningdek, Nyuton chelaki deb ham ataladi) haqiqiy aylanish harakatini tananing bevosita atrofdagi jismlarga nisbatan nisbiy aylanishi sifatida aniqlash mumkin emasligini koʻrsatish uchun ishlab chiqilgan. Bu „haqiqiy harakat va dam olish“ ning „xususiyatlari, sabablari va oqibatlari“ dan beshta dalildan biri boʻlib, uning fikrini qoʻllab-quvvatlaydi, bu umuman olganda, haqiqiy harakat va dam olishni boshqa jismlarga nisbatan harakat yoki dam olishning alohida holatlari sifatida belgilash mumkin emas., lekin buning oʻrniga faqat mutlaq fazoga mos yozuvlar bilan aniqlanishi mumkin. Shu bilan bir qatorda, ushbu tajribalar " mutlaq aylanish " deganda nimani anglatishini aniq taʼriflaydi va „ nimaga nisbatan aylanish?“ [1] Umumiy nisbiylik mutlaq fazodan va sababi tizimdan tashqarida boʻlgan fizikadan, fazo-vaqt geodeziyasi tushunchasidan voz kechadi. [2]
Koʻnikmalar
Ushbu dalillar va mutlaq va nisbiy vaqt, makon, joy va harakat oʻrtasidagi farqlar muhokamasi Nyutonning "Tabiiy falsafaning matematik asoslari" (1687) asarining 1-kitobining „Taʼriflar“ boʻlimlari oxiridagi maktabda keltirilgan. Klassik mexanikaning asoslarini yaratgan va uning universal tortishish qonunini kiritgan, sayyoralar harakatining birinchi miqdoriy adekvat dinamik izohini bergan, III kitobning oxiridagi General Scholium bilan chalkashtirib yuboriladi. [3]
Toʻgʻri chiziqli inertsiya printsipini qabul qilishlariga va koʻrinadigan harakatning kinematik nisbiyligini tan olishlariga qaramay (bu Ptolemey yoki Kopernik tizimining toʻgʻri ekanligiga asoslanadi), XVII asrning tabiat faylasuflari haqiqiy harakat va dam olishni jismoniy jihatdan alohida tavsiflovchilar sifatida koʻrib chiqishda davom etdilar. individual tananing. Nyuton qarshi boʻlgan hukmron qarash Rene Dekart tomonidan ishlab chiqilgan va (qisman) Gotfrid Leybnits tomonidan qoʻllab-quvvatlangan. U boʻsh makonni metafizik imkonsiz deb hisobladi, chunki fazo materiyaning kengayishidan boshqa narsa emas, yoki boshqacha qilib aytganda, narsalar orasidagi boʻshliq haqida gapirganda, aslida bu narsalar oʻrtasidagi munosabatlarga ishora qilinadi va bu narsalar oʻrtasidagi munosabatlar emas. ular orasida turgan baʼzi bir shaxsga. [4] [5] Yuqoridagi tushunchaga muvofiq, jismning harakati haqidagi har qanday daʼvo vaqt oʻtishi bilan tavsifga tushadi, bunda koʻrib chiqilayotgan jism t 1 da, bir guruh „orqaviy“ jismlar yaqinida topiladi va qandaydir t 2 da topiladi. baʼzi boshqa „moʻljal“ moddasi yoki jismlari yaqinida. [6] [7]
Dekart, harakatlanuvchi qismlari boʻlgan va dastlab atrofdagi halqaga nisbatan tinch holatda boʻlgan jismning oʻzi halqaga nisbatan maʼlum bir burchak tezligiga tezlashtirilgan vaziyat va boshqa vaziyat oʻrtasida haqiqiy farq boʻlishini tan oldi. bu atrofdagi halqaga markaziy ob’ektga nisbatan teskari tezlanish berilgan. Faqatgina markaziy ob’ekt va uning atrofidagi halqani hisobga olgan holda, markaziy ob’ekt ham, uning atrofidagi halqa ham mutlaqo qattiq jismlar deb hisoblasak, harakatlar bir-biridan farq qilmaydi. Biroq, agar markaziy ob’ekt ham, uning atrofidagi halqa ham mutlaqo qattiq boʻlmasa, ulardan birining yoki ikkalasining qismlari aylanish oʻqidan uchib ketishga moyil boʻladi.
Inkvizitsiya bilan bogʻliq boʻlgan shartli sabablarga koʻra, Dekart harakatni ham mutlaq, ham nisbiy deb aytdi. [8] 19-asrning oxiriga kelib, barcha harakatlarning nisbiy ekanligi haqidagi bahs, xususan, Ernst Mach (1883) tomonidan qayta kiritildi. [9] [10]
Shunga ko'ra, biz jism o'z yo'nalishini va tezligini "kosmosda" o'zgarmagan holda saqlaydi, desak, bizning tasdiqimiz "butun olam"ga qisqartirilgan ishoradan ko'proq yoki kam emas.
Munozara
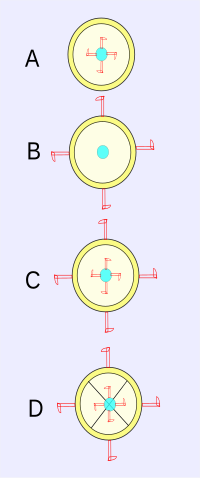
[tahrir | manbasini tahrirlash]Nyuton chelakni muhokama qilmoqda (lotincha: situla) shnur bilan osilgan suv bilan toʻldirilgan. [11] Agar shnur oʻziga mahkam buralib, keyin chelak qoʻyib yuborilsa, u nafaqat eksperimentatorga, balki uning tarkibidagi suvga nisbatan ham tez aylana boshlaydi. (Bu holat yuqoridagi B diagrammasiga mos keladi.)
Ushbu bosqichdagi nisbiy harakat eng katta boʻlsa-da, suv yuzasi tekis boʻlib qoladi, bu suv qismlarining chelakka yaqin boʻlishiga qaramay, nisbiy harakat oʻqidan chekinish tendentsiyasiga ega emasligini koʻrsatadi. Oxir-oqibat, shnur yechilishda davom etar ekan, suv yuzasi eksperimentatorga nisbatan chelakning aylanayotgan harakatiga ega boʻlib, botiq shaklga ega boʻladi. Bu konkav shakli suvning paqirga nisbatan tinch holatda boʻlishiga qaramay, suvning aylanishini koʻrsatadi. Boshqacha aytganda, harakatlar faqat nisbiy boʻlishi mumkin, mutlaq harakat boʻlmaydi, degan fikrdan farqli oʻlaroq, chelak va suvning nisbiy harakati emas, balki suvning botiqligiga sabab boʻladi. (Bu holat D diagrammasiga toʻgʻri keladi.) Ehtimol, suvning konkavligi boshqa narsaga nisbatan aylanishni koʻrsatadi: mutlaq boʻshliq deylikmi? Nyuton shunday deydi: „Suvning haqiqiy va mutlaq aylanma harakatini aniqlash va oʻlchash mumkin“. [12]
1846 yilda Endryu Motning Nyuton soʻzlarining tarjimasida: [13]
Agar uzun shnur bilan osilgan idish tez-tez aylantirilsa, shnur qattiq buralib, keyin suv bilan to'ldiriladi va suv bilan birga dam oladi; keyin, boshqa bir kuchning to'satdan ta'sirida, u teskari yo'l bilan aylanib qoladi va shnur o'z-o'zidan buralib ketayotganda, idish bir muncha vaqt bu harakatni davom ettiradi; suv yuzasi dastlab tekis bo'ladi, xuddi idish harakatlana boshlaganidan oldin; Ammo kema asta-sekin o'z harakatini suvga etkazish orqali uni oqilona aylana boshlaydi va asta-sekin orqaga chekinadi va idishning yon tomonlariga ko'tarilib, o'zini botiq shaklga aylantiradi ... Suvning bu ko'tarilishi o'z harakat o'qidan chekinishga intilishini ko'rsatadi; va bu yerda nisbiyga to'g'ridan-to'g'ri zid bo'lgan suvning haqiqiy va mutlaq aylana harakati o'zini ochib beradi va bu harakat bilan o'lchanishi mumkin. ... Shunday qilib, bu harakat suvning atrofdagi jismlarga nisbatan har qanday tarjimasiga bog'liq emas va haqiqiy aylanma harakatni bunday tarjima bilan aniqlab bo'lmaydi. ...; lekin nisbiy harakatlar ... hech qanday real ta'sirdan umuman mahrum. ... Haqiqatan ham, alohida jismlarning haqiqiy harakatlarini zohiriydan aniqlash va ularni samarali farqlash juda qiyin masala; chunki o'sha harakatsiz bo'shliqning bu harakatlar amalga oshiriladigan qismlari hech qanday holatda bizning his-tuyg'ularimiz kuzatuviga tushmaydi.
— Isaac Newton; Principia, Book 1: Scholium
Harakatning nisbiy emas, mutlaq ekanligi haqidagi argument toʻliq emas, chunki u tajribaga tegishli ishtirokchilarni faqat chelak va suv bilan cheklaydi, bu cheklov oʻrnatilmagan. Darhaqiqat, suvning konkavligi tortishish kuchini aniq oʻz ichiga oladi va buning natijasida Yer ham ishtirok etadi. Bu yerda faqat nisbiy harakat oʻrnatilganligini taʼkidlagan Makning tanqidi: [14]
Nyutonning suvning aylanadigan idishi bilan tajribasi shunchaki bizga ma'lum qiladiki, suvning idishning yon tomonlariga nisbatan nisbiy aylanishi sezilarli markazdan qochma kuchlarni keltirib chiqarmaydi, lekin bunday kuchlar uning er massasiga nisbatan nisbiy aylanishi natijasida hosil bo'ladi. va boshqa samoviy jismlar.
— Ernst Max, L. Bouquiaux Leybnits asarida keltirgan., p. 104
Maxning gipotezasini umumiy nisbiylik nazariyasida integrasiyalash darajasi Max printsipi maqolasida muhokama qilinadi; Umuman olganda, umumiy nisbiylik toʻliq Machian emas, deb qabul qilinadi.
Barcha kuzatuvchilar aylanayotgan suvning yuzasi egri ekanligiga rozi. Biroq, bu egrilikning tushuntirishi barcha kuzatuvchilar uchun markazdan qochma kuchni oʻz ichiga oladi, bundan mustasno, haqiqiy statsionar kuzatuvchi bundan mustasno, bu egrilik suvning aylanish tezligiga mos kelishini aniqlaydi va qoʻshimcha markazdan qochma kuchga ehtiyoj sezmaydi. Shunday qilib, statsionar ramka aniqlanishi mumkin va „Nimaga nisbatan statsionar?“:
Asl savol, "harakat qonunlari qanday mos yozuvlar doirasiga nisbatan?" noto'g'ri qo'yilganligi ma'lum bo'ldi. Harakat qonunlari uchun mohiyatan mos yozuvlar tizimi sinfini va (printsipial ravishda) ularni qurish tartibini "aniqlash".[15]
Xuddi shu maqsadda mutlaq aylanishning paydo boʻlishini aniqlashga qaratilgan qoʻshimcha fikrlash tajribasi ham Nyuton tomonidan taklif qilingan: ikkita bir xil sharni ularning ogʻirlik markazi atrofida aylanayotgan va ip bilan bogʻlanganligini kuzatish misoli. Ipdagi kuchlanishning paydo boʻlishi mutlaq aylanishdan dalolat beradi; aylanuvchi sharlarga qarang.
Batafsil tahlil
[tahrir | manbasini tahrirlash]
Aylanadigan chelak tajribasining tarixan qiziq boʻlishi uning suv yuzasi shaklini kuzatish orqali mutlaq aylanishni aniqlash mumkinligini koʻrsatishda foydalidir. Biroq, aylanish bu oʻzgarishga qanday olib keladi, degan savol tugʻilishi mumkin. Quyida chelakdagi aylanuvchi suv yuzasining konkavligini tushunishning ikkita yondashuvi keltirilgan.

Nyutonning harakat qonunlari
[tahrir | manbasini tahrirlash]Chelakdagi aylanuvchi suyuqlik sirtining shakli sirt elementiga turli kuchlar uchun Nyuton qonunlari yordamida aniqlanishi mumkin. Masalan, Knudsen va Xyortga qarang. [16] Tahlil suvning harakatsiz koʻrinadigan birgalikda aylanadigan ramkadagi erkin tana diagrammasi bilan boshlanadi. Suvning balandligi h = h (r) aylanish oʻqidan r radial masofaning funktsiyasidir va maqsad bu funktsiyani aniqlashdir. Sirtdagi suv hajmining elementi uchta kuchga taʼsir qilishi koʻrsatilgan: tortishish kuchi taʼsirida vertikal kuch F g, gorizontal, radial tashqi markazdan qochma kuch F Cfgl va suv yuzasiga normal kuch F n . tanlangan sirt elementini oʻrab turgan suvning qolgan qismi. Atrofdagi suv taʼsiridan kelib chiqadigan kuch suv yuzasi uchun normal ekanligi maʼlum, chunki muvozanatdagi suyuqlik siljish kuchlanishlarini ushlab turolmaydi. [17] Entoni va Brakettdan iqtibos keltirish uchun: [18]
Bir xil zichlikdagi suyuqlikning yuzasi..., agar tinch holatda bo'lsa, hamma joyda kuch chiziqlariga perpendikulyar bo'ladi; chunki agar bunday bo'lmasa, sirtdagi bir nuqtadagi kuch ikkita komponentga, biri perpendikulyar, ikkinchisi esa sirtga teginish bo'lishi mumkin edi. Ammo suyuqlikning tabiatiga ko'ra, tangensial kuch suyuqlikning harakatini o'rnatadi, bu suyuqlik tinch holatda ekanligi haqidagi bayonotga ziddir.
— Uilyam Arnold Entoni va Cyrus Fogg Brackett: Fizikadan boshlang'ich darslik. , p. 127
Bundan tashqari, suv elementi harakat qilmagani uchun, barcha uch kuchning yigʻindisi nolga teng boʻlishi kerak. Nolga tenglashtirish uchun suvning kuchi markazdan qochma va tortishish kuchlarining yigʻindisiga qarama-qarshi boʻlishi kerak, yaʼni suv yuzasi bu yoʻnalishdagi normal nuqtalarini sozlashi kerak. (Juda oʻxshash muammo — bu burilishning nishabi mashina yoʻldan sirgʻalib ketmasligi uchun oʻrnatiladigan burilish dizayni. Aylanadigan chelak holatidagi oʻxshashlik shundan iboratki, suv sathining elementi sirtning normali F g + F Cfgl vektor qoʻshilishi natijasida hosil boʻlgan vektor natijasiga toʻgʻri kelmasa, sirtni yuqoriga yoki pastga „siljitadi“.)
r ning ortishi bilan markazdan qochma kuchi nisbatga koʻra ortadi (tenglamalar massa birligiga yoziladi):
bu yerda Ω — suvning doimiy aylanish tezligi. Ogʻirlik kuchi da oʻzgarmaydi
Bu yerda g — tortishish taʼsiridan tezlanish . Bu ikki kuch qoʻshilib, berilgan vertikaldan ph burchak ostida natija hosil qiladi
r ortishi bilan aniq katta boʻladi. Ushbu natija suv yuzasi uchun normal boʻlishini taʼminlash va shuning uchun suv ostidagi suv kuchi bilan samarali ravishda nolga teng boʻlishini taʼminlash uchun sirt normasi bir xil burchakka ega boʻlishi kerak, yaʼni
sirt shakli uchun oddiy differensial tenglamaga olib keladi:
yoki yigʻindi:
Bu yerda h (0) — r = 0 da suvning balandligi. Boshqacha qilib aytganda, suv yuzasi radiusga bogʻliq boʻlgan parabolikdir.
Potensial energiya
[tahrir | manbasini tahrirlash]Birgalikda aylanuvchi ramkada markazdan qochma kuch bilan bogʻliq boʻlgan potentsial energiya haqidagi qiziqarli gʻoyadan foydalanib, suv sathining shakli boshqacha, juda intuitiv tarzda topilishi mumkin. Ω burchak tezligida bir tekis aylanadigan mos yozuvlar tizimida xayoliy markazdan qochma kuch konservativ boʻlib, quyidagi koʻrinishdagi potentsial energiyaga ega: [19] [20]
bu yerda r — aylanish oʻqidan radius. Ushbu natijani radial tashqi kuchni olish uchun potentsialning gradientini olish orqali tekshirish mumkin:
Potensial energiyaning (saqlangan ish) maʼnosi shundan iboratki, sinov jismining kattaroq radiusdan kichikroq radiusga harakatlanishi markazdan qochma kuchga qarshi ishni bajarishni va shu bilan potentsial energiyani olishni oʻz ichiga oladi. Ammo balandligi pastroq boʻlgan kichikroq radiusdagi bu sinov tanasi endi ekvivalent tortishish potentsial energiyasini yoʻqotdi.
Shuning uchun potentsial energiya aylanadigan chelakdagi suv sathining konkavligini tushuntiradi. Eʼtibor bering, muvozanat holatida sirt shunday shaklga ega boʻladiki, uning yuzasining istalgan joyidagi hajm elementi boshqa har qanday joydagi kabi bir xil potentsial energiyaga ega. Demak, sirtdagi suvning hech bir elementi pozitsiyani koʻchirishga undamaydi, chunki barcha pozitsiyalar energiya jihatidan tengdir. Yaʼni muvozanatga erishiladi. Boshqa tomondan, agar energiya kamroq boʻlgan sirt mintaqalari mavjud boʻlsa, yuqori potentsial energiyaning sirt joylarini egallagan suv past energiyali pozitsiyalarni egallashga harakat qiladi, chunki ideal suyuqlikda lateral harakatlanish uchun hech qanday toʻsiq yoʻq.
Biz suvning sirt shaklini bir lahzaga oʻzgartirib, uni teng energiyali sirtdan farq qilish uchun ushbu muvozanat holatini ataylab buzishni tasavvur qilishimiz mumkin. Shaklning bu oʻzgarishi barqaror boʻlmaydi va suv bizning sunʼiy ravishda yaratilgan shaklda qolmaydi, balki paqirning yon tomonlariga yoki choʻqqisiga tegib, ideal boʻlmagan ishqalanish kuchlari paydo boʻlguncha koʻp shakllarni vaqtinchalik oʻrganish bilan shugʻullanadi. suyuqlikning ideal boʻlmagan tabiati, tebranishlarni oʻldiradi va suv muvozanat shakliga joylashadi.
Ishda teng energiyali sirt printsipini koʻrish uchun chelakning aylanish tezligini noldan asta-sekin oshirishni tasavvur qiling. Suv yuzasi dastlab tekis va teng potentsial energiya yuzasi aniq, chunki sirtdagi barcha nuqtalar suvga taʼsir qiluvchi tortishish maydonida bir xil balandlikda joylashgan. Baʼzi kichik burchakli aylanish tezligida esa, er usti suvining elementi markazdan qochma kuch taʼsirida tashqariga harakatlanib, kamroq potentsial energiyaga erishishi mumkin; Yerning markaziga yaqinroq tortishish kuchi bilan harakatlanayotgan jismni tasavvur qiling: ob’ekt kuchga moslashish orqali oʻzining potentsial energiyasini pasaytiradi. Suv siqilmaydigan va chelak chegaralarida qolishi kerakligi sababli, bu tashqi harakat kattaroq radiusda suvning chuqurligini oshiradi, kattaroq radiusda sirt balandligini oshiradi va kichikroq radiusda uni pasaytiradi. Suv yuzasi biroz konkav boʻlib qoladi, buning natijasida kattaroq radiusdagi suvning potentsial energiyasi kattaroq balandlikka erishish uchun tortishish kuchiga qarshi bajarilgan ish tufayli ortadi. Suv balandligi oshgani sayin, periferiya tomon harakatlanish foydali boʻlmaydi, chunki markazdan qochma kuch bilan ishlashda potentsial energiyaning kamayishi tortishish kuchiga qarshi ishlaydigan energiyaning koʻpayishi bilan muvozanatlanadi. Shunday qilib, maʼlum burchakli aylanish tezligida konkav sirt barqaror vaziyatni ifodalaydi va aylanish qanchalik tez boʻlsa, bu sirt shunchalik konkav boʻladi. Agar aylanish toʻxtatilsa, konkav sirtni shakllantirishda saqlanadigan energiya, masalan, ishqalanish orqali, muvozanat tekis yuzani tiklashdan oldin yoʻqolishi kerak.
Doimiy potensial energiya yuzasini miqdoriy jihatdan amalga oshirish uchun suvning balandligi boʻlsin : u holda tortishish kuchining birlik massasiga potentsial energiyasi va sirtdagi massa birligiga toʻgʻri keladigan umumiy potentsial energiya
bilan r dan mustaqil fon energiya darajasi. Statik vaziyatda (aylanuvchi ramkada suyuqlikning harakati yoʻq), bu energiya r holatidan qatʼiy nazar doimiydir. Energiya doimiy boʻlishini talab qilib, biz parabolik shaklni olamiz:
Bu yerda h(0) bu r = 0 (oʻq) dagi balandlik. 1 va 2-rasmlarga qarang.
Sentrifuganing ishlash printsipini potentsial energiyaning ushbu ifodasi nuqtai nazaridan ham oddiy tushunish mumkin, bu aylanish oʻqidan uzoqroq hajmni ogʻirroq modda egallaganida u energiya jihatidan qulay ekanligini koʻrsatadi.
- ↑ Disalle, Robert. The Cambridge Companion to Newton Cohen: . Cambridge University Press, 2002 — 43-bet. ISBN 0-521-65696-6.
- ↑ Gilson, James G. (September 1, 2004), Mach's Principle II, arXiv:physics/0409010, Bibcode:2004physics...9010G
- ↑ See the Principia on line at Andrew Motte translation, pp. 77-82.
- ↑ Descartes, René. Descartes: Selected Philosophical Writings. Cambridge University Press, 1988 — 191-bet. ISBN 0-521-35812-4.
- ↑ Alexandre Koyre. From the Closed World to the Infinite Universe. Forgotten Books, 1957 — 75-bet. ISBN 1-60620-143-3.
- ↑ René Descartes. Principia Philosophiae, 1664.
- ↑ Daniel Garber. Descartes' Metaphysical Physics. University of Chicago Press, 1992 — 170-bet. ISBN 0-226-28219-8.
- ↑ Robert Disalle. Understanding Space-time: The philosophical development of physics from Newton to Einstein. Cambridge University Press, 2006 — 19-bet. ISBN 0-521-85790-2.
- ↑ Mach, E. (1960 [1883]), The Science of Mechanics, LaSalle, IL: Open Court Publishing, p. 284.
- ↑ Ignazio Ciufolini, John Archibald Wheeler. Gravitation and Inertia. Princeton University Press, 1995 — 386–387-bet. ISBN 0-691-03323-4.
- ↑ For a discussion of Newtonʼs original argument, see Max Born & Günther Leibfried. Einstein's Theory of Relativity. New York: Courier Dover Publications, January 1962 — 78–79-bet. ISBN 0-486-60769-0.
- ↑ Robert Disalle „Newton's philosophical analysis of space and time“, . op. cit. I. Bernard Cohen, George Edwin Smith: , 25 April 2002 — 45-bet. ISBN 0-521-65696-6.
- ↑ See the Principia on line at Andrew Motte Translation pp. 79-81
- ↑ Bouquiaux, L.. Leibniz Dascal: . Springer, 2008 — 104-bet. ISBN 978-1-4020-8667-0.
- ↑ Robert DiSalle „Space and Time: Inertial Frames“, . The Stanford Encyclopedia of Philosophy Edward N. Zalta: , Summer 2002.
- ↑ Jens M. Knudsen, Poul G. Hjorth. Elements of Newtonian Mechanics, 3rd, Springer, 2000 — 143-bet. ISBN 3-540-67652-X.
- ↑ Lawrence S. Lerner. Physics for Scientists and Engineers. Jones & Bartlett, 1997 — 404-bet. ISBN 0-86720-479-6.
- ↑ William Arnold Anthony & Cyrus Fogg Brackett. Elementary Text-book of Physics. Wiley, 1884 — 127-bet. „pascal's law.“
- ↑ Robert Daniel Carmichael. The Theory of Relativity. John Wiley & Sons, 1920 — 78-bet. „fictitious Christoffel potential.“
- ↑ Hans J. Weber & George B. Arfken. Essential mathematical methods for physicists. Academic Press, 2003 — 79-bet. ISBN 0-12-059877-9.
Manbalar
[tahrir | manbasini tahrirlash]- Brian Greene „Chapter 2, The Universe and the Bucket“, . The Fabric of the Cosmos: Space, Time, and the Texture of Reality. A A Knopf, 2004. ISBN 0-375-41288-3.
- The isotropy of the cosmic background radiation is another indicator that the universe does not rotate. See:
- R. B. Partridge. 3 K: The Cosmic Microwave Background Radiation. Cambridge University Press, 1995 — 279–280-bet. ISBN 0-521-35254-1. [sayt ishlamaydi]
- D. Lynden-Bell. Relativistic Astrophysics, Igor' Dmitrievich Novikov, Bernard Jean Trefor Jones, Draza Marković (Editors), 1996 — 167-bet. ISBN 0-521-62113-5.
- Ralph A. Alpher and Robert Herman. Big bang cosmology and the cosmic black-body radiation, in Proc. Am. Philos. Soc. vol. 119, no. 5 (1975), 1975 — 325–348-bet. ISBN 9781422371077.
Havolalar
[tahrir | manbasini tahrirlash]- Newtonʼs Views on Space, Time, and Motion Stenford falsafa entsiklopediyasidan, Robert Rynasevichning maqolasi. Ushbu maqolaning oxirida asl lotin matniga nisbatan tarjimalardagi nozik farqlarning yoʻqolishi muhokama qilinadi.
- Life and Philosophy of Leibniz see section on Space, Time and Indiscernibles Leybnits kosmosning sababchi agent sifatida harakat qilish gʻoyasiga qarshi bahs yuritishi uchun.
- Newtonʼs Bucket Suv shaklini aks ettiruvchi interaktiv applet va ushbu maqolada keltirilganidan koʻra toʻliqroq suv shakli modelining matematik hosilasi bilan biriktirilgan PDF fayli.















