Plank qonuni
Fizikada Plank qonuni jism va uning muhiti oʻrtasida materiya yoki energiyaning aniq oqimi boʻlmaganda, maʼlum bir haroratda termal muvozanatda boʻlgan qora jism tomonidan chiqarilgan elektromagnit nurlanishning spektral zichligini T.
19-asrning oxirida fiziklar nima uchun aniq oʻlchangan qora jism nurlanishining kuzatilgan spektri mavjud nazariyalar tomonidan bashorat qilinganidan yuqori chastotalarda sezilarli darajada farq qilishini tushuntirib bera olmadilar. 1900-yilda nemis fizigi Maks Plank evristik yoʻl bilan kuzatilgan spektr formulasini chiqardi va qora jism nurlanishini oʻz ichiga olgan boʻshliqdagi faraziy elektr zaryadlangan osilator oʻz energiyasini u bilan bogʻliq elektromagnit toʻlqin chastotaga proporsional boʻlgan minimal oʻsishda E ga oʻzgartirishi mumkin, deb taxmin qildi. Plank dastlab energiyani oʻsishga boʻlish gipotezasini faqat toʻgʻri javob olish uchun kiritilgan matematik hunarmandchilik deb hisoblagan boʻlsa-da, boshqa fiziklar, shu jumladan Albert Eynshteyn ham uning ishiga asoslanishdi va Plankning tushunchasi endi kvant nazariyasi uchun muhim ahamiyatga ega ekanligi eʼtirof etildi.
Formulasi
[tahrir | manbasini tahrirlash]Har bir jismoniy jism oʻz-oʻzidan va uzluksiz ravishda elektromagnit nurlanish chiqaradi va tananing spektral nurlanishi, Bν, maʼlum bir radiatsiya chastotasi uchun birlik maydoniga, birlik qattiq burchakka, chastota birligiga toʻgʻri keladigan spektral emissiya quvvatini tavsiflaydi. Quyida keltirilgan Plankning radiatsiya qonuni bilan berilgan munosabat shuni koʻrsatadiki, harorat ortishi bilan tananing umumiy nurlanish energiyasi ortadi va tarqaladigan spektrning choʻqqisi qisqaroq toʻlqin uzunliklariga siljiydi. Bunga koʻra, T absolyut haroratda ν chastotasi uchun jismning spektral nurlanishi quyidagicha ifodalanadi.
Bu yerda kB — Boltsman doimiysi, h — Plank doimiysi va c — moddiy yoki vakuumdagi yorugʻlik tezligi . Bν ning SI birliklari W·sr−1·m−2·Hz−1 dir.
Spektral nurlanish chastota birligi oʻrniga toʻlqin uzunligi birligi λ boʻyicha ham ifodalanishi mumkin. Bundan tashqari, qonun boshqa atamalar bilan ifodalanishi mumkin, masalan, maʼlum bir toʻlqin uzunligida chiqarilgan fotonlar soni yoki nurlanish hajmidagi energiya zichligi.
Past chastotalar chegarasida (yaʼni uzun toʻlqin uzunliklarida) Plank qonuni Reyl-Jins qonuniga, yuqori chastotalar (yaʼni kichik toʻlqin uzunliklari) chegarasida esa Vienga yaqinlashishiga intiladi.
Maks Plank 1900-yilda qonunni faqat empirik aniqlangan konstantalar bilan ishlab chiqdi va keyinchalik energiya taqsimoti sifatida ifodalangan termodinamik muvozanatdagi nurlanish uchun yagona barqaror taqsimot ekanligini koʻrsatdi. Energiya taqsimoti sifatida u Bose-Eynshteyn taqsimoti, Fermi-Dirak taqsimoti va Maksvell-Boltzmann taqsimotini oʻz ichiga olgan termal muvozanat taqsimotlari oilasidan biridir.
Qora jism radiatsiyasi
[tahrir | manbasini tahrirlash]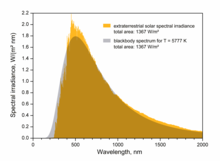
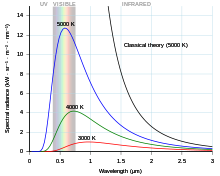
Qora jism — bu barcha nurlanish chastotalarini oʻzlashtiradigan va chiqaradigan ideallashtirilgan obyekt. Termodinamik muvozanatga yaqin joyda chiqariladigan nurlanish Plank qonuni bilan yaqindan tavsiflanadi va uning haroratga bogʻliqligi sababli Plank nurlanishi termal nurlanish deb ataladi, shuning uchun tananing harorati qanchalik baland boʻlsa, u har bir toʻlqin uzunligida shunchalik koʻp radiatsiya chiqaradi.
Plank nurlanishi jismning haroratiga bogʻliq boʻlgan toʻlqin uzunligida maksimal intensivlikka ega. Masalan, xona haroratida (~300 K), jism asosan infraqizil va koʻrinmas boʻlgan termal nurlanish chiqaradi. Yuqori haroratlarda infraqizil nurlanish miqdori ortadi va issiqlik sifatida sezilishi mumkin va koʻproq koʻrinadigan nurlanish chiqariladi, shuning uchun jism koʻrinadigan darajada qizil porlaydi. Yuqori haroratlarda jism yorqin sariq yoki koʻk-oq rangga ega boʻlib, ultrabinafsha va hatto rentgen nurlarini oʻz ichiga olgan qisqa toʻlqinli nurlanishni sezilarli darajada chiqaradi. Quyosh yuzasi (~6000 K) ham infraqizil, ham ultrabinafsha nurlanishni katta miqdorda chiqaradi; uning emissiyasi koʻrinadigan spektrda eng yuqori nuqtaga etadi. Harorat tufayli sodir boʻlgan bu siljish Vienning siljish qonuni deb ataladi.
Plank nurlanishi — bu termal muvozanatdagi har qanday jismning kimyoviy tarkibi yoki sirt tuzilishi qanday boʻlishidan qatʼi nazar, uning yuzasidan chiqaradigan eng katta nurlanish miqdori. Nurlanishning muhitlar orasidagi interfeys orqali oʻtishi interfeysning emissiyasi (haqiqiy nurlanishning nazariy Plank nurlanishiga nisbati) bilan tavsiflanishi mumkin, odatda ε belgisi bilan belgilanadi. Umuman olganda, u kimyoviy tarkibga va fizik tuzilishga, haroratga, toʻlqin uzunligiga, oʻtish burchagiga va qutblanishga bogʻliq. Tabiiy interfeysning emissiyasi har doim ε = 0 va 1 orasida.
Har ikkisi ε = 1 boʻlgan va unga tushgan barcha nurlanishni oʻzlashtiradigan boshqa muhit bilan bogʻlangan jismga qora jism deyiladi. Qora jismning sirtini har bir toʻlqin uzunligida mukammal aks ettirmaydigan shaffof boʻlmagan devorlari bilan bir xil haroratda saqlanadigan katta korpus devoridagi kichik teshik orqali modellashtirish mumkin. Muvozanat holatida bu korpus ichidagi nurlanish, kichik tuynukdan chiqadigan nurlanish kabi Plank qonuni bilan tavsiflanadi.
Maksvell-Boltzman taqsimoti issiqlik muvozanatidagi moddiy zarrachalar gazi uchun yagona maksimal entropiya energiyasi taqsimoti boʻlgani kabi, fotonlar gazi uchun Plank taqsimoti ham shundaydir. Zarrachalar massasi va soni muhim rol oʻynaydigan moddiy gazdan farqli oʻlaroq, termal muvozanatdagi foton gazining spektral nurlanishi, bosimi va energiya zichligi butunlay harorat bilan belgilanadi.
Agar foton gazi Plank boʻlmasa, termodinamikaning ikkinchi qonuni oʻzaro taʼsirlar (fotonlar va boshqa zarralar yoki hatto, etarlicha yuqori haroratlarda, fotonlarning oʻzlari oʻrtasidagi) foton energiya taqsimotining oʻzgarishiga va Plank taqsimotiga yaqinlashishga olib kelishini kafolatlaydi. Termodinamik muvozanatga bunday yondashuvda fotonlar muvozanat haroratiga yetguncha boʻshliqni Plank taqsimoti bilan toʻldirish uchun kerakli sonlarda va toʻgʻri energiya bilan yaratiladi yoki yoʻq qilinadi. Goʻyo gaz quyi gazlar aralashmasi boʻlib, toʻlqin uzunligining har bir bandi uchun bittadan va har bir kichik gaz oxir-oqibat umumiy haroratga erishadi.
Bν(ν, T) miqdori harorat va chastotaga bogʻliq boʻlgan spektral nurlanishdir. SI tizimida W·m−2·sr−1·Hz−1 birliklari mavjud. Cheksiz kichik quvvat miqdori Bν(ν, T) cos θ dA dΩ dν cheksiz kichik sirt maydoni dA dan normal sirtdan θ burchak bilan tasvirlangan yoʻnalishda cheksiz kichik chastota diapazonida cheksiz kichik qattiq burchakka dΩ nurlanadi. dν chastota boʻyicha markazlashtirilgan ν . Har qanday qattiq burchakka tarqaladigan umumiy quvvat Bν(ν, T) ning ushbu uchta kattalikdagi integralidir va Stefan-Boltzman qonuni bilan berilgan. Qora jismdan Plank nurlanishining spektral nurlanishi qutblanishning har bir yoʻnalishi va burchagi uchun bir xil qiymatga ega va shuning uchun qora jism Lambert radiatori deyiladi.
Formulaning turli xil shakllari
[tahrir | manbasini tahrirlash]Plank qonunini turli fan sohalarining konvensiyalari hamda afzalliklariga qarab bir necha shakllarda uchratish mumkin. Spektral nurlanish qonunining turli shakllari quyidagi jadvalda jamlangan. Chapdagi shakllar koʻpincha eksperimental sohalarda, oʻngdagilar esa nazariy sohalarda koʻp uchraydi.
| h bilan | ħ bilan | ||
|---|---|---|---|
| oʻzgaruvchan | tarqatish | oʻzgaruvchan | tarqatish |
| Chastotasiν | Burchak chastotasiω | ||
| Toʻlqin uzunligiλ | Burchakli toʻlqin uzunligiy | ||
| Toʻlqin soni
ν̃ |
Burchakli toʻlqin raqami
k |
||
Ushbu taqsimotlar qora jismlarning spektral nurlanishini ifodalaydi — chiqaradigan yuzadan chiqariladigan quvvat, chiqaradigan sirtning proeksiyalangan maydoni, birlik qattiq burchak, spektral birlik (chastota, toʻlqin uzunligi, toʻlqin soni yoki ularning burchak ekvivalentlari). Nurlanish izotropik (yaʼni yoʻnalishdan mustaqil) boʻlgani uchun, normal burchak ostida chiqarilgan quvvat proyeksiya qilingan maydonga, shuning uchun Lambertning kosinus qonuniga binoan bu burchakning kosinusiga proporsionaldir va qutbsizdir.
Manbalar
[tahrir | manbasini tahrirlash]- Radiatsiya haqida qisqacha maʼlumot
- Qora jism nurlanishi — Plank qonuni bilan tanishish uchun interaktiv simulyatsiya
- Plank qonuni boʻyicha fan olamiga kirish
Bu maqola birorta turkumga qoʻshilmagan. Iltimos, maqolaga aloqador turkumlar qoʻshib yordam qiling. (Aprel 2024) |







