Romb

Romb (qadimgi yunoncha: ῥόμβος, lotincha: rombus „doira“) — barcha tomonlari teng boʻlgan to'rtburchak. Burchaklari toʻgʻri burchaklardan iborat boʻlgan romb kvadrat deb ataladi.

Romb (yunoncha: rombos — pirildoq, aylanuvchi) — tomonlari oʻzaro teng boʻlgan yassi toʻrtburchak (rasmga q.). Rombning xossalari: 1) diagonallari oʻzaro perpendikulyar; 2) Rombning diagonallari uning burchaklarini teng ikkiga boʻladi. Rombning diagonallari kesishgan nuqta uning simmetriya markazidir. Rombga ichki aylana chizish mumkin. Rombning yuzi uning diagonallari koʻpaytmasining yarmiga teng. Burchaklaridan biri a boʻlgan Rombning yuzi 5=a2sina. Hamma burchaklari 90° boʻlgan Romb kvadratidir.

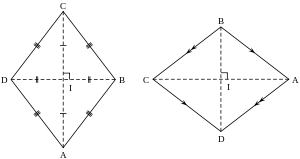
Asosiy xossalari

• Romb parallelogramm hisoblanadi, chunki uning qarama-qarshi tomonlari oʻzaro paralleldir: AV || CD, AD || VS.
• Romb diagonallari bir birini toʻgʻri burchak hosil qilgan holda kesib oʻtishadi (AC ⊥ BD) va kesib oʻtish nuqtasida teng ikkiga boʻlinishadi.
• Romb diagonallari uning burchaklarining bissektrisalari hisoblanadi (∠DCA = ∠BCA, ∠ABD = ∠CBD va hokazo)
• Romb diagonnallarining kvadratlari yigʻindisi toʻrtga koʻpaytirilgan tomonining kvadratiga teng (masalan: AC² + BD² = 4 • AD²).

Asosiy alomatlari

Parallelogramm ABCD romb hisoblanadi, agarda:

• uning barcha tomonlari teng boʻlsa: AB = BC = CD = AD
• uning diagonallari bir birini toʻgʻri burchak hosil qilgan holda kesib oʻtsa

Yana qarang

• Geometriya
• Parallel
• kvadrat