Muvozanatlashgan to‘p

Sakrab turgan toʻp. Harakat havo qarshiligi tufayli juda parabolik emas.

Muvozanatlashgan toʻpning fizikasi sakrab tushayotgan toʻplarning jismoniy xatti-harakatlariga, xususan uning boshqa jismning yuzasiga taʼsir qilishdan oldin, paytida va keyin harakatiga taalluqlidir. Oʻrta maktab yoki bakalavriat darajasidagi fizika kurslarida sakrab turgan toʻp harakatining bir qancha jihatlari mexanikaga kirish boʻlib xizmat qiladi. Biroq, xulq-atvorni aniq modellashtirish murakkab va sport muhandisligiga qiziqish uygʻotadi.

Toʻpning harakati odatda snaryad harakati bilan tavsiflanadi (u tortishish kuchi, tortishish, Magnus effekti va suzuvchanlik taʼsirida boʻlishi mumkin), va uning taʼsiri odatda qayta tiklash koeffitsienti bilan tavsiflanadi (bu tabiatga taʼsir qilishi mumkin). toʻp, taʼsir qiluvchi sirtning tabiati, zarba tezligi, aylanish va harorat va bosim kabi mahalliy sharoitlar). Halol oʻyinni taʼminlash uchun koʻplab sport boshqaruv organlari oʻz toʻplarining sakrashiga cheklovlar qoʻyishadi va toʻpning aerodinamik xususiyatlarini buzishni taqiqlaydi. Toʻplarning tebranishi Mezoamerikan toʻp oʻyini kabi qadimiy sportning oʻziga xos xususiyati boʻlgan.

Parvoz paytidagi kuchlar va harakatga taʼsiri

Aylanayotgan toʻpning uchishi vaqtida unga taʼsir qiluvchi kuchlar tortishish kuchi (F _G), tortish kuchi (F _D), Magnus kuchi (F _M) va suzuvchi kuch (F _B).

Sakrab chiqayotgan toʻpning harakati snaryad harakatiga boʻysunadi. Haqiqiy toʻpga koʻp kuchlar, yaʼni tortishish kuchi (F _G), havo qarshiligidan kelib chiqadigan tortish kuchi (F _D), toʻpning aylanishidan kelib chiqadigan Magnus kuchi (F _M) va suzuvchi kuch (F _B) taʼsir qiladi. . Umuman olganda, toʻpning harakatini tahlil qilish uchun barcha kuchlarni hisobga olgan holda Nyutonning ikkinchi qonunidan foydalanish kerak:

${\begin{aligned}\sum \mathbf {F} &=m\mathbf {a} ,\\\mathbf {F} _{\text{G}}+\mathbf {F} _{\text{D}}+\mathbf {F} _{\text{M}}+\mathbf {F} _{\text{B}}&=m\mathbf {a} =m{\frac {d\mathbf {v} }{dt}}=m{\frac {d^{2}\mathbf {r} }{dt^{2}}},\end{aligned}}$

bu yerda m — toʻpning massasi. Bu yerda a, v, r toʻpning t vaqt boʻyicha tezlanishi, tezligi va holatini ifodalaydi.

Gravitatsiya

Toʻpning zarbadan keyin 70 ° burchak ostida sakrash traektoriyasi

Gravitatsion kuch pastga yoʻnaltirilgan va quyidagiga teng.

$F_{\text{G}}=mg,$

Bu yerda m — toʻpning massasi va g — tortishish tezlanishi, Yerda 7000976399999999999♠9.764 m/s² orasida oʻzgarib turadi.7000976399999999999♠9.764 m/s² va 7000983400000000000♠9.834 m/s² . Boshqa kuchlar odatda kichik boʻlganligi sababli, harakat koʻpincha faqat tortishish taʼsirida boʻlgandek ideallashtiriladi . Agar toʻpga faqat tortishish kuchi taʼsir etsa, uning parvozi paytida mexanik energiya saqlanib qoladi. Bu ideallashtirilgan holatda harakat tenglamalari berilgan:

${\begin{aligned}\mathbf {a} &=-g\mathbf {\hat {j}} ,\\\mathbf {v} &=\mathbf {v} _{\text{0}}+\mathbf {a} t,\\\mathbf {r} &=\mathbf {r} _{0}+\mathbf {v} _{0}t+{\frac {1}{2}}\mathbf {a} t^{2},\end{aligned}}$

bu yerda a, v va r toʻpning tezlanishi, tezligi va holatini, v ₀ va r ₀ esa mos ravishda toʻpning boshlangʻich tezligi va holatini bildiradi.

Aniqroq qilib aytadigan boʻlsak, agar toʻp yer bilan θ burchak ostida sakrab tushsa, x — va y — oʻqlaridagi harakat (mos ravishda gorizontal va vertikal harakatni ifodalaydi) bilan tavsiflanadi.

x oʻqi	y oʻqi
${\begin{aligned}a_{\text{x}}&=0,\\v_{\text{x}}&=v_{0}\cos \left(\theta \right),\\x&=x_{0}+v_{0}\cos \left(\theta \right)t,\end{aligned}}$	${\begin{aligned}a_{\text{y}}&=-g,\\v_{\text{y}}&=v_{0}\sin \left(\theta \right)-gt,\\y&=y_{0}+v_{0}\sin \left(\theta \right)t-{\frac {1}{2}}gt^{2}.\end{aligned}}$

Tenglamalar shuni koʻrsatadiki, tekis yuzada sakrab turgan toʻpning maksimal balandligi (H) va masofasi (R) va parvoz vaqti (T) bilan berilgan.

${\begin{aligned}H&={\frac {v_{0}^{2}}{2g}}\sin ^{2}\left(\theta \right),\\R&={\frac {v_{0}^{2}}{g}}\sin \left(2\theta \right),~{\text{and}}\\T&={\frac {2v_{0}}{g}}\sin \left(\theta \right).\end{aligned}}$

Toʻpning harakatini yanada takomillashtirish havo qarshiligini (shuningdek, tortish va shamol kabi tegishli taʼsirlarni), Magnus effektini va suzish qobiliyatini hisobga olgan holda amalga oshirilishi mumkin. Yengilroq toʻplar tezroq tezlashgani sababli, ularning harakatiga bunday kuchlar koʻproq taʼsir qiladi.

Tortilishi

Toʻp atrofidagi havo oqimi Reynolds soniga (Re) qarab laminar yoki turbulent boʻlishi mumkin, bu quyidagicha aniqlanadi:

${\text{Re}}={\frac {\rho Dv}{\mu }},$

bu yerda ρ havoning zichligi, μ havoning dinamik yopishqoqligi, D toʻpning diametri va v havo orqali toʻpning tezligi. 7002293150000000000♠20 °C haroratda7002293150000000000♠20 °C, ρ = 7000120000000000000♠1.2 kg/m³ va μ = 6995180000000000000♠1.8×10⁻⁵ Pa·s.

Agar Reynolds soni juda past boʻlsa (Re<1), toʻpni tortish kuchi Stokes qonuni bilan tavsiflanadi:

$F_{\text{D}}=6\pi \mu rv,$

bu yerda r - toʻpning radiusi. Bu kuch toʻp yoʻnalishiga qarama-qarshi harakat qiladi (yoʻnalishi boʻyicha $\textstyle -{\hat {\mathbf {v} }}$ ). Koʻpgina sport toʻplari uchun Reynolds soni 10 ⁴ va 10 ⁵ orasida boʻladi va Stokes qonuni qoʻllanilmaydi. Reynolds sonining yuqori qiymatlarida toʻpni tortish kuchi oʻrniga tortish tenglamasi bilan tavsiflanadi:

$F_{\text{D}}={\frac {1}{2}}\rho C_{\text{d}}Av^{2},$

Bu yerda C _d — tortish koeffitsienti va A - toʻpning koʻndalang kesimi maydoni.

Surish toʻpning parvoz paytida mexanik energiyasini yoʻqotishiga olib keladi va uning masofasi va balandligini pasaytiradi, oʻzaro shamol esa uni dastlabki yoʻlidan buradi. Ikkala effekt ham golf kabi sport oʻyinchilari tomonidan hisobga olinishi kerak.

Magnus effekti

Orqaga burilish bilan toʻpga taʼsir qiluvchi Magnus kuchi. Jingalak oqim chiziqlari turbulent uygʻonishni ifodalaydi. Havo oqimi aylanish yoʻnalishi boʻyicha burilib ketgan.

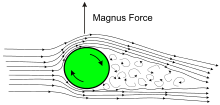
  Toʻpning aylanishi Magnus effekti orqali uning traektoriyasiga taʼsir qiladi. Kutta-Jukovski teoremasiga koʻra, havo oqimi aniq boʻlmagan aylanayotgan shar uchun Magnus kuchi ga teng.

$F_{\text{M}}={\frac {8}{3}}\pi r^{3}\rho \omega v,$

Bu yerda r — toʻpning radiusi, ω toʻpning burchak tezligi (yoki aylanish tezligi), ρ havo zichligi va v - toʻpning havoga nisbatan tezligi. Bu kuch harakatga perpendikulyar va aylanish oʻqiga perpendikulyar (yoʻnalishda) yoʻnaltiriladi. $\textstyle {\hat {\mathbf {\omega } }}\times {\hat {\mathbf {v} }}$). Orqaga aylanish uchun kuch yuqoriga, tepaga aylanish uchun esa pastga yoʻnaltiriladi. Aslida, oqim hech qachon oʻzgarmasdir va Magnus lifti tomonidan yaxshiroq tasvirlangan.

$F_{\text{M}}={\frac {1}{2}}\rho C_{\text{L}}Av^{2},$

bu yerda ρ — havo zichligi, C _L koʻtarish koeffitsienti, A toʻpning tasavvurlar maydoni va v toʻpning havoga nisbatan tezligi. Koʻtarish koeffitsienti murakkab omil boʻlib, u boshqa narsalar qatorida r ω / v nisbati, Reynolds soni va sirt pürüzlülüğüne bogʻliq. Muayyan sharoitlarda lift koeffitsienti hatto salbiy boʻlishi mumkin, bu Magnus kuchining yoʻnalishini oʻzgartiradi (teskari Magnus effekti).

Tennis yoki voleybol kabi sport turlarida oʻyinchi parvoz paytida toʻpning traektoriyasini (masalan, topspin yoki backspin orqali) boshqarish uchun Magnus effektidan foydalanishi mumkin. Golfda bu effekt odatda golfchiga zarar keltiradigan kesish va bogʻlash uchun javobgardir, lekin ayni paytda haydovchi va boshqa tortishish oraligʻini oshirishga yordam beradi. Beysbolda koʻzalar kavisli toʻplar va boshqa maxsus maydonlarni yaratish uchun effektdan foydalanadilar.

Toʻpni buzish koʻpincha noqonuniy hisoblanadi va koʻpincha 2006 yil avgust oyida Angliya va Pokiston oʻrtasidagi kriket bahslari markazida boʻladi. Beysbolda " tupurish " atamasi toʻpning aerodinamikasini oʻzgartirish uchun toʻpni tupurish yoki boshqa moddalar bilan noqonuniy qoplashni anglatadi.

Suzuvchanlik

Suv yoki havo kabi suyuqlikka botgan har qanday ob’ekt yuqoriga qarab suzuvchanlikni boshdan kechiradi. Arximed printsipiga koʻra, bu suzuvchi kuch jism tomonidan almashtirilgan suyuqlikning ogʻirligiga teng. Sfera holatida bu kuch ga teng:

$F_{\text{B}}={\frac {4}{3}}\pi r^{3}\rho g.$

Suzuvchi kuch odatda tortish va Magnus kuchlariga nisbatan kichik boʻlib, koʻpincha eʼtiborsiz qolishi mumkin. Biroq, basketbolda suzuvchi kuch toʻp ogʻirligining taxminan 1,5% ni tashkil qilishi mumkin. Suzuvchanlik yuqoriga yoʻnaltirilganligi sababli, u toʻpning masofasini va balandligini oshiradi.

Taʼsiri

Sirtga taʼsir qiladigan sharning siqilishi (A→B) va dekompressiyasi (B→C). Taʼsir kuchi odatda siqish masofasiga mutanosibdir, hech boʻlmaganda kichik siqilishlar uchun va bahor kuchi sifatida modellashtirilishi mumkin.

Tashqi mediafayllar
	Florian Korn. „Ball bouncing in slow motion: Rubber ball“. YouTube (2013).

Toʻp sirtga taʼsir qilganda, sirt orqaga buriladi va tebranadi, toʻp ham tovush va issiqlik hosil qiladi va toʻp kinetik energiyani yoʻqotadi. Bundan tashqari, zarba toʻpga bir oz aylanishni berishi mumkin va uning translatsiya kinetik energiyasining bir qismini aylanish kinetik energiyasiga oʻtkazishi mumkin. Ushbu energiya yoʻqolishi odatda (bilvosita) qayta tiklash koeffitsienti (yoki COR, e bilan belgilanadi) orqali tavsiflanadi:

$e=-{\frac {v_{\text{f}}-u_{\text{f}}}{v_{\text{i}}-u_{\text{i}}}},$

bu yerda v _f va v _i toʻpning yakuniy va boshlangʻich tezliklari, u _f va u _{i esa} mos ravishda sirtga taʼsir etuvchi oxirgi va boshlangʻich tezliklardir. Toʻp koʻchmas yuzaga taʼsir qilganda, COR soddalashtiriladi

$e=-{\frac {v_{\text{f}}}{v_{\text{i}}}}.$

Toʻp polga tushirilganda, COR 0 (sakrash yoʻq, energiya yoʻqolishi) va 1 (mukammal sakrash, energiya yoʻqotilishi) oʻrtasida oʻzgaradi. 0 dan past yoki 1 dan yuqori boʻlgan COR qiymati nazariy jihatdan mumkin, lekin toʻp sirtdan oʻtganini (e < 0) yoki toʻp unga taʼsir qilganda sirt „boʻshashmagan“ligini koʻrsatadi (e > 1) prujinali platformaga toʻpning qoʻnish holati.

Harakatning vertikal va gorizontal qismlarini tahlil qilish uchun COR baʼzan oddiy COR (e_y) va tangensial COR (e _x) ga boʻlinadi, sifatida aniqlanadi.

$e_{\text{y}}=-{\frac {v_{\text{yf}}-u_{\text{yf}}}{v_{\text{yi}}-u_{\text{yi}}}},$

$e_{\text{x}}=-{\frac {(v_{\text{xf}}-r\omega _{\text{f}})-(u_{\text{xf}}-R\Omega _{\text{f}})}{(v_{\text{xi}}-r\omega _{\text{i}})-(u_{\text{xi}}-R\Omega _{\text{i}})}},$

Bu yerda r va ω toʻpning radiusi va burchak tezligini, R va Ω esa radiusni va burchak tezligini taʼsir qiluvchi sirtni (masalan, beysbol tayoqchasi) bildiradi. Xususan , r ω shar yuzasining tangensial tezligi, R Ω esa taʼsir qiluvchi sirtning tangensial tezligidir. Bular, ayniqsa, toʻp sirtga qiya burchak ostida taʼsir qilganda yoki aylanish ishtirok etganda qiziqish uygʻotadi.

Toʻpga faqat tortishish kuchi taʼsir qiladigan aylanmasdan erga toʻgʻridan-toʻgʻri tushish uchun COR bir nechta boshqa miqdorlar bilan bogʻlanishi mumkin:

$e=\left|{\frac {v_{\text{f}}}{v_{\text{i}}}}\right|={\sqrt {\frac {K_{\text{f}}}{K_{\text{i}}}}}={\sqrt {\frac {U_{\text{f}}}{U_{\text{i}}}}}={\sqrt {\frac {H_{\text{f}}}{H_{\text{i}}}}}={\frac {T_{\text{f}}}{T_{\text{i}}}}={\sqrt {\frac {gT_{\text{f}}^{2}}{8H_{\text{i}}}}}.$

Bu yerda K va U toʻpning kinetik va potensial energiyasini bildiradi, H — toʻpning maksimal balandligi va T — toʻpning uchish vaqti. „I“ va „f“ pastki belgisi toʻpning dastlabki (zarbadan oldin) va yakuniy (zarbadan keyin) holatini bildiradi. Xuddi shunday, zarba paytida energiya yoʻqolishi COR bilan bogʻliq boʻlishi mumkin

${\text{Energy Loss}}={\frac {{K_{\text{i}}}-{K_{\text{f}}}}{K_{\text{i}}}}\times 100\%=\left(1-e^{2}\right)\times 100\%.$

Toʻpning COR ga bir nechta narsa taʼsir qilishi mumkin, asosan

• taʼsir qiluvchi sirtning tabiati (masalan, oʻt, beton, sim toʻr)
• toʻpning materiali (masalan, charm, kauchuk, plastmassa)
• toʻp ichidagi bosim (boʻshliq boʻlsa)
• zarba paytida toʻpning aylanish miqdori
• zarba tezligi

Harorat kabi tashqi sharoitlar taʼsir qiluvchi sirt yoki toʻpning xususiyatlarini oʻzgartirishi mumkin, bu ularni yanada moslashuvchan yoki qattiqroq qiladi. Bu, oʻz navbatida, CORga taʼsir qiladi. Umuman olganda, toʻp yuqori zarba tezligida koʻproq deformatsiyalanadi va shunga mos ravishda oʻz energiyasini koʻproq yoʻqotadi va CORni kamaytiradi.

Spin va taʼsir burchagi

Taʼsir paytida aylanayotgan toʻpga taʼsir qiluvchi kuchlar tortishish kuchi, normal kuch va ishqalanish kuchidir (umuman, „tarjima“ va „aylanish“ komponentiga ega). Agar sirt burchakli boʻlsa, tortishish kuchi sirtdan burchak ostida boʻladi, boshqa kuchlar esa sirtga perpendikulyar yoki parallel boʻlib qoladi.

Yerga taʼsir qilganda, baʼzi translasyonel kinetik energiya aylanma kinetik energiyaga va aksincha, toʻpning zarba burchagi va burchak tezligiga qarab aylanishi mumkin. Agar toʻp zarba paytida gorizontal harakat qilsa, ishqalanish toʻpning harakatiga qarama-qarshi yoʻnalishda „tarjima“ komponentga ega boʻladi. Rasmda toʻp oʻngga harakat qilmoqda va shuning uchun u toʻpni chapga itarib yuboradigan ishqalanishning tarjima komponentiga ega boʻladi. Bundan tashqari, agar toʻp zarba bilan aylansa, ishqalanish toʻpning aylanishiga qarama-qarshi yoʻnalishda „aylanuvchi“ komponentga ega boʻladi. Rasmda toʻp soat yoʻnalishi boʻyicha aylanmoqda va erga taʼsir qiladigan nuqta toʻpning massa markaziga nisbatan chapga siljiydi. Shunday qilib, ishqalanishning aylanish komponenti toʻpni oʻngga itaradi. Oddiy kuch va tortishish kuchidan farqli oʻlaroq, bu ishqalanish kuchlari toʻpga moment taʼsir qiladi va uning burchak tezligini oʻzgartiradi (ω).

Adabiyotlar

• Briggs, L. J. (1945). "Methods for measuring the coefficient of restitution and the spin of a ball". Journal of Research of the National Bureau of Standards 34 (1): 1–23. doi:10.6028/jres.034.001. 
• Cross, R.. Physics of Baseball & Softball. Springer, 2011. ISBN 978-1-4419-8112-7. 
• Cross, R. „Physics of bounce“. Sydney University (2014-yil iyun).
• Cross, R. (2015). "Behaviour of a bouncing ball". Physics Education 50 (3): 335–341. doi:10.1088/0031-9120/50/3/335. 
• Stronge, W. J.. Impact mechanics. Cambridge University Press, 2004. ISBN 978-0-521-60289-1. 
• Erlichson, Herman (1983). "Maximum projectile range with drag and lift, with particular application to golf". American Journal of Physics 51 (4): 357–362. doi:10.1119/1.13248. https://www.forbes.com/sites/stevensalzberg/2013/04/29/the-physics-of-golf-whats-the-ideal-loft-to-hit-the-ball-farthest/#5c150bf26926. Qaraldi: 29 April 2013. Muvozanatlashgan to‘p]]

Manbalar

• Whittington, E. M., ed. (2001). The Sport of Life and Death: The Mesoamerican Ballgame. Thames & Hudson. ISBN 0-500-05108-9.
• Brancazio, P. J. (1985). „Trajectory of a fly ball“. The Physics Teacher. 23 (1): 20-23. Bibcode:1985PhTea..23…20B. doi:10.1119/1.2341702.
• Walker, J. (2014). Fundamentals of Physics (10th Extended ed.). John Wiley & Sons. Figure 4-8, p. 70. ISBN 978-1-118-23072-5.
• Bush, J. W. M. (2013). „The aerodynamics of the beautiful game“ (PDF). In Clanet, C. (ed.). Sports Physics. Les Éditions de l'École Polytechnique. p. 171. hdl:1721.1/87576. ISBN 978-2-7302-1615-9.
• Hirt, C.; Claessens, S.; Fecher, T.; Kuhn, M.; Pail, R.; Rexer, M. (2013). „New ultrahigh-resolution picture of Earth’s gravity field“. Geophysical Research Letters. 40 (16): 4279-4283. Bibcode:2013GeoRL..40.4279H. doi:10.1002/grl.50838.
• Nave, R. „Trajectories“. HyperPhysics. Retrieved 2017-01-27.
• „Dry air properties“. The Engineering Toolbox. Retrieved 2017-02-11.
• Southard, J. (Fall 2006). „Chapter 3: Flow past a sphere II: Stokeʼs law, the Bernoulli equation, turbulence, boundary layers, flow separation“ (PDF). Special Topics: An Introduction to Fluid Motions, Sediment Transport, and Current-generated Sedimentary Structures. MIT. pp. 35-82. Archived from the original (PDF) on 2017-02-05.